Excel関数を勉強するために、とりあえず全部の関数を使用して、使用方法をメモするという自己満足記事です。
一気に全て書くのは難しいため随時追記をしていきます。
ABS関数
=ABS(数値)
数値:絶対値を求める数値を指定する
概要
引数で与えられた数値の絶対値を返します。
例えば、-2が引数に与えられれば2を返却し、2が引数に与えられればそのまま2を返します。
結構使いそうなイメージですが、意外と業務で使ったことはないですね。マイナスをプラスとして計算すること自体があまりないのかもしれない。
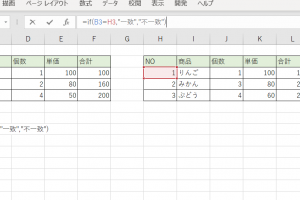
使用例

B2に設定されている式
=ABS(A2)ACCRINT関数
=ACCRINT(発行日,最初の利払日,受渡日,利率,額面,頻度,[基準],[計算方式])
発行日:証券の発行日を指定する
初回利払日: 証券の利息が最初に支払われる日付を指定する
受渡日:証券の受渡日を指定する
利率:証券の年利を指定する
額面:証券の額面価格を指定する
頻度:年間の利息支払回数を指定する
基準(省略可能):計算に使用する基準日数を示す数値を指定を指定する(※1)
計算方式(省略可能):1は、発行日から受渡日までの未収利息の合計。0は、初回利払日から受渡日までの未収利息を返す。
※1基準日数の計算
| 設定値 | 説明 |
|---|---|
| 0 または省略 | 30 日/360 日 (NASD 方式) |
| 1 | 実際の日数/実際の日数 |
| 2 | 実際の日数/360 日 |
| 3 | 実際の日数/365 日 |
| 4 | 30 日/360 日 (ヨーロッパ方式) |
概要
証券の未収利息額を返却します。
未収利息額とは簿記の勘定科目の1つで「既に利息は発生しているが、当期に受け取れないので時期に計上する」というもののようです。
この関数では証券で発生した利益を計算することが出来ます。
財務関係でExcelを使用した経験があまりないので使用したことがないですね。
使用例

B8に設定されている式
=ACCRINT(B2,B3,B4,B5,B6,B7)ACCRINTM関数
=ACCRINTM(発行日,受渡日,利率,額面,基準)
発行日:証券の発行日を指定する
受渡日:証券の受渡日を指定する
利率:証券の年利を指定する
額面:証券の額面価格を指定する
基準(省略可能):計算に使用する基準日数を示す数値を指定を指定する(※1)
※1基準日数の計算 (ACCRINT関数と同じ)
| 設定値 | 説明 |
|---|---|
| 0 または省略 | 30 日/360 日 (NASD 方式) |
| 1 | 実際の日数/実際の日数 |
| 2 | 実際の日数/360 日 |
| 3 | 実際の日数/365 日 |
| 4 | 30 日/360 日 (ヨーロッパ方式) |
概要
証券の未収利息額を返却するのですが、ACCRINT関数と異なるのが、こちらは特定の受渡日に受けるのではなく満額を受け取る場合の計算になります。
満額(Mangaku)の頭文字がMなので、 ACCRINTにMがつくと満額計算になると覚えればよさそうでしょうかw
使い方はほぼACCRINTと同じですが、受渡日が満期になるので引数が少なくなっています。
こちらも、 財務関係でExcelを使用したことがないので存在自体を知らなかった関数ですね。
使用例

B6に設定されている式
=ACCRINTM(B2,B3,B4,B5)ACOS関数
=ACOS(数値)
数値:コサインの値
概要
引数で与えた数値のアークコサインの値を返却します。
高校数学で習った人も多いと思いますが、 コサインとは直角三角形における辺の長さの比率を表したものです。

上記の表で言うとB/Aがコサインになるかと思います。
このコサインの値は角度が決まることで一意に決めることが出来ます。例として、コサインが√3/2の場合は角度は30度になります。
アークコサインとは 、特定のコサインになる角度のことです。
ちなみに結果はラジアンで戻ってくるので、必要に応じてDEGREES関数を使用して角度の値に変換します。
使用例
コサインの値が0.5になる角度を求める

B3に設定されている式
=DEGREES(ACOS(B2))ACOSH関数
=ACOSH(数値)
数値:双曲線関数に与える値(x軸)
概要
双曲線余弦関数 (ハイパボリックコサイン) に対応した双曲角を求める関数です。
まず、 双曲線正弦関数とは以下の式で与える事ができます。

その際に、 特定のハイパボリックコサインの値になる双曲角の角度を関数で求めることが出来ます。
使用例

B3に設定されている式
=ACOSH(B2)ACOT関数
=ACOT(数値)
数値:求める角度のコタンジェント
概要
引数で与えた数値のアークコタンジェントの値を返却します。
三角関数に関する関数が続いていますが、コタンジェントとは高校数学などで習うタンジェントの逆数を示します。

上記のA/Bがタンジェントのはずなので、今回使用するコタンジェントはB/Aになるかと思います。
アークコタンジェントなので 、コタンジェントの値を引数に入れて、そのコタンジェントになる角度を戻します。
このACOT関数も他の三角関数と同様に、結果はラジアンで戻ってくるので、必要に応じてDEGREES関数を使用して角度の値に変換します。
使用例

=DEGREES(ACOT(G57))ACOTH関数
=ACOTH(数値)
数値:逆双曲線余接に与える値(x軸)
概要
逆双曲線余接 (ハイパーボリック・アーク・コタンジェント) に対応した双曲角を求める関数です。
ここまで来るとよくわからないですが、双曲線関数のtanh(ハイパーボリックタンジェント)の逆数なのでアークがついて、ハイパーボリック・アーク・コタンジェントということですね。
使用例

B3に設定されている式
=ACOTH(B2)ADDRESS関数
=ADDRESS(行番号,列番号,[参照の型],[参照形式],[シート名])
行番号:アドレスを表示したいセルの行番号
列番号:アドレスを表示したいセルの列番号
参照の型(省略可):返されるアドレスが絶対参照か相対参照かを指定(※1)
参照形式(省略可):TRUEまたは省略でA1、FALSEでR1C1形式で返す)
シート名(省略可):アドレスにシート名を付与して返却する
※1参照形式
| 参照の型 | 結果として返される参照形式 | |
|---|---|---|
| 1 または省略 | 絶対参照 | |
| 2 | 行は絶対参照、列は相対参照 | |
| 3 | 行は相対参照、列は絶対参照 | |
| 4 | 相対参照 |
概要
数値で指定した行番号、列番号からアドレスを返却する。
ここまで数学や経理の関数ばかりだったので、ようやくExcelに関する関数が出てきましたね。
第3引数の絶対参照、相対参照はアドレスの前に”$”がつくかどうかが変化します。($がつくとオートフィルで値が変更されない)
第4引数はA1形式かR1C1形式のどちらで戻すかを指定します。

使い道としては、数値を戻す関数(ROWなど)やINDIRECT関数と組わせて動的に参照先を変えるような事ができるかと思います。
使用例

B6に設定されている式
=INDIRECT(ADDRESS(B4,B5))AGGREGATE関数
=AGGREGATE(集計方法, オプション, 範囲)
集計方法:集計を行う方法(※1)
オプション:関数の検証範囲内の無視する値(※2)
範囲:集計するセルがある範囲
※1集計方法
| 集計方法 | 求める値 | 同じ機能の関数 |
|---|---|---|
| 1 | 平均を求める | AVERAGE |
| 2 | 数値の個数を求める | COUNT |
| 3 | データの個数を求める | COUNTA |
| 4 | 最大値を求める | MAX |
| 5 | 最小値を求める | MIN |
| 6 | 積を求める | PRODUCT |
| 7 | 不偏標準偏差を求める | STDEV.S |
| 8 | 標本標準偏差を求める | STDEV.P |
| 9 | 合計を求める | SUM |
| 10 | 不偏分散を求める | VAR.S |
| 11 | 標本分散を求める | VAR.P |
| 12 | 中央値を求める | MEDIAN |
| 13 | 最頻値を求める | MODE.SNGL |
| 14 | 大きい方からの順位を求める | LARGE |
| 15 | 小さい方からの順位を求める | SMALL |
| 16 | 百分位数を求める | PERCENTILE.INC |
| 17 | 四分位数を求める | QUARTILE.INC |
| 18 | 百分位数を求める(0%と100%を除く) | PERCENTILE.EXC |
| 19 | 四分位数を求める(0%と100%を除く) | QUARTILE.EXC |
※2オプション
| オプション | 動作 |
|---|---|
| 0 または省略 | ネストされた SUBTOTAL 関数と AGGREGATE 関数を無視します。 |
| 1 | 非表示の行、ネストされた SUBTOTAL 関数と AGGREGATE 関数を無視します。 |
| 2 | エラー値、ネストされた SUBTOTAL 関数と AGGREGATE 関数を無視します。 |
| 3 | 非表示の行、エラー値、ネストされた SUBTOTAL 関数と AGGREGATE 関数を無視します。 |
| 4 | 何も無視しません。 |
| 5 | 非表示の行を無視します。 |
| 6 | エラー値を無視します。 |
| 7 | 非表示の行とエラー値を無視します。 |
概要
AGGREGATEは集計を行う関数です。
集計内容は、引数の1つ目で与えられる数値によって決まるのですが、例えば「平均」や「最大値」などがあります。
ですが、EXCELには既にAVERAGE関数やMAX関数があるため、そちらを使用しても同じ動作をすることが出来ます。
と言うかAGGREGATEで実装できる動きは、全て他の関数で代用することが出来ます。
ではAGGREGATE関数の存在意義は何かというと、動的に集計結果を変えられるということですね。例えばリスト選択で「最小値、最大値、平均」というものを定義しておいて、その選択肢によって集計方法を変えることが出来ます。
使用例

C6に設定されている式
=AGGREGATE(C4,C5,C1:C3)AMORDEGRC関数
=AMORDEGRC(取得価額, 購入日, 開始期, 残存価額, 期, 率, [基準])
取得価額:コスト、購入したときの金額
購入日:購入を実施した日
開始期:最初の会計期が終了する日
残存価額:耐用年数が終了したときの価格
期:会計期 (会計年度)
利率:減価償却率
基準(省略可):1 年を何日として計算するか(※1)
※1基準
| 基準 | 1 年の日数 |
|---|---|
| 0 または省略 | 360 日 (NASD 方式) |
| 1 | 実際の日数 |
| 3 | 365 日 |
| 4 | 360 日 (ヨーロッパ方式) |
概要
各会計期における減価償却費を計算して表示する関数です。
減価償却費には様々な計算方法があり
- 定額法(取得価額×耐用年数)
- 定率法(前期末の帳簿価額× 償却率)
などがあります。
このAMORDEGRC関数で用いられる計算式はフランスの会計システム用ということです。
まあ、まず使うことはなさそうですね…。
使用例

B7に設定されている式
=AMORDEGRC(B1,B2,B3,B4,B5,B6)AMORLINC関数
=AMORDEGRC(取得価額, 購入日, 開始期, 残存価額, 期, 率, [基準])
取得価額:コスト、購入したときの金額
購入日:購入を実施した日
開始期:最初の会計期が終了する日
残存価額:耐用年数が終了したときの価格
期:会計期 (会計年度)
利率:減価償却率
基準(省略可):1 年を何日として計算するか(※1)
※1基準
| 基準 | 1 年の日数 |
|---|---|
| 0 または省略 | 360 日 (NASD 方式) |
| 1 | 実際の日数 |
| 3 | 365 日 |
| 4 | 360 日 (ヨーロッパ方式) |
概要
各会計期における減価償却費を計算して表示します。
ただ、この計算はフランスの会計システムのみで使われます。
あれ?この説明は既に書いた気がしたのですが…
一つ前の「AMORDEGRC関数」と全く同じですね。相違点としては、
- AMORDEGRC→耐用年数による減価償却係数を計算に含める
- AMORLINC→耐用年数による減価償却係数を計算に含めない
という違いのようです。実際には減価償却はあり得ると思うのでAMORDEGRCのほうが実用的な気がしますね。
(いずれにしても日本だと使用しない気がしますが…)
使用例

B7に設定されている式
=AMORLINC(B1,B2,B3,B4,B5,B6)AND関数
=AND(論理式1、論理式2…)
論理式1、論理式2…:複数指定可。指定した論理式が全てTRUEならAND関数もTRUEを返す
概要
引数を複数指定でき、その引数が全てTRUEであるかどうかを検査する関数です。
1つでもFALSEの論理式が引数に与えられた時点で、AND関数が返す値もFALSEになります。
IF文で分岐する場合にはかなり使用することになるかと思います。例えばセルA1の値が1~9の間である場合には
A1<10
A1>0
の両方を検査する必要があるので、AND関数を使うことになります。
=IF(AND(A1<10,A1>0),”範囲内です”,”範囲外です”)
引数の数は不定なので配列関数とも非常に相性が良いです。EXACTと組み合わせて範囲内が完全一致するかどうかなど。
{=AND(EXACT(C1:C3,D1:D3))}
↑C1~C3がD1~D3と等しいか検査する
使用例

B2に設定されている式
=IF(AND(B1<10,B1>0),"範囲内です","範囲外です")ARABIC関数
=ARABIC(ローマ字)
ローマ字:アラビア数字に変換するローマ数字
概要
引数でローマ数字を渡すと、その値をアラビア数字に変換して返してくれます。
ローマ数字とは、以下の形の数字です。ゲームのタイトルとかでよく見たことがありますね。
I、II、III
これを普段使用しているアラビア数字に直してくれるのがこの関数です。
ローマ数字はXが10になり、Lが50、Cが100、Mが1000となるので、MCLXの場合は1000+100+50+10で1160になります。
ちなみに引数は小文字でも大文字でも可のようです。上記例であれば、MCLXでもmclxでもOKということです。
使用例

B2に設定されている式
=ARABIC(B1)AREAS関数
=AREAS(範囲)
範囲:領域の数を数える範囲
概要
引数で指定された範囲にある領域の数を返却します。
領域とは聞き慣れない言葉ですが、連続したセル範囲のことを指します。連続したセル範囲は以下の画像を見てもらうのが早いと思います。

B2~D4(青い範囲)
E5(赤い範囲)
F6:I9(紫の範囲)
合計で3つの領域が選択されているので、戻り値は3です。つまり連続したセル範囲とは四角で表現できる範囲と考えれば良さそうです。
使用する場面としては、重なりがあるかを検出したい場合が殆どになるかなと思っています。下記の使用例では重なりがあるので返却値が引数の個数と一致しません。
使用例

↑上記の結果は2となります。(E5はB2:E5と重なっているため3にならない)
A1に設定されている式
=AREAS(E5 (B2:D4,E5,B2:E5))ASC関数
=ASC(全角英数カナ)
全角英数カナ:半角に変換するカナ文字
概要
全角英数カナを半角カナに変換する関数。凄くシンプルな関数なのでわかりやすいですね。
用途としては、システム上の制限で半角しか入れられない項目に対して変換を行うというのがほとんどになりそうです。
また、この関数を使用して「英数カナでが入っているか?」のチェックもできそうです。
=(ASC(B1)=B1)
上記式により、仮に英数カナが入ると一致しなくなるのでFALSEが帰るようになります。
(実際には「全て漢字かひらがな」というチェックは少ないかもですが)
使用例

B2に設定されている式
=ASC(B1)ASIN関数
=ASIN(数値)
数値:求める角度のアークサイン
概要
引数で与えたアークサインの角度を返却します。
アークサインとは高校数学などで習うサインの逆数になるので、三角関数の図で表すと…

上記画像でB/Aになるかと思います。
他の三角関数と同様に、結果はラジアンで戻ってくるので、普通はDEGREES関数を使用して角度の値に変換します。
使用例

B2に設定されている式
=DEGREES(ASIN(A1))ASINH関数
=ASINH(数値)
数値:逆双曲線正弦に与える値(x軸)
概要
双曲線逆正弦 (ハイパーボリックサインの逆関数)に対応した双曲角を求める関数です。
まず、 双曲線逆正弦とは以下の式で与える事ができます。

その際に、 特定のハイパーボリックサインの値になる双曲角の角度を関数で求めることが出来ます。
使用例

B2に設定されている式
=ASINH(B1)ATAN関数
=ATAN(数値)
数値:アークタンジェントの値
概要
引数に与えた数値に対するアークタンジェント (逆正接) の角度を戻します。
上の方で書いているASINやACOSと同じで角度を返してくれるのですが、ラジアンで戻ってくるので必要に応じてDEGREES関数を使用して角度の値に変換します。
ちなみになぜかアークタンジェントのみATAN2という関数が用意されていて、座標指定もできます。(後述します)
使用例

B2に設定されている式
=DEGREES(ATAN(B1))ATAN2関数
=ATAN2(x座標, y座標)
x座標:ATANのX座標
y座標:ATANのY座標
概要
引数に与えた座標に対するアークタンジェント (逆正接) の角度を戻します。
1つ前で書いたATAN関数の座標指定バージョン。
x座標とy座標が決まればアークタンジェントの値も一意になるので、必要なのか微妙なところ。
実際の測定結果などは座標がインプットになることが多いから用意されているのだろうか。
使用例

B3に設定されている式
=DEGREES(ATAN2(B1,B2))ATANH関数
=ATANH(数値)
数値:求める双曲線逆正接の値
概要
引数で与えた数値に対する双曲線逆正接を返却します。
双曲線逆正接とはハイパーボリックタンジェントの逆関数となるので、=ATANH (TANH (数値))と書き換えることも出来ます。
使用例

B2に設定されている式
=ATANH(B1)AVEDEV関数
=AVEDEV(数値 1, [数値 2], …)
数値:複数の指定が可能
概要
引数に1つ以上の数値を取り、その数値の絶対偏差の平均値を返却します。
数値指定はSUM関数などと同様に、1つずつカンマまで区切ってもいいし、「A1:A5」みたいに範囲を指定してもいいです。
平均絶対偏差は、ばらつきを求める際に使用する数式で、実績値と平均値の差の絶対値の平均値です。
言葉で書くとややこしいですが、仮に10、20、30、(平均20)の場合は
((20-10) + (20-20) + (30-20)) / 3 = 20 / 3 = 6.6
三角関数型をやった後だと楽に感じるなあw
使用例

B4に設定されている式
=AVEDEV(B1:B3)AVERAGE関数
=AVERAGE(数値)
数値:平均値を求める数値(複数指定可)
概要
引数に1つ以上の数値を取り、その数値の平均値を返却します。
平均とは説明するまでもないですが、数値の合計/個数で求められる値です。
仮に10、20、30の場合は
(10+20+30) / 3 = 20
となります。これはよく使う関数ですね。
使用例

B4に設定されている式
=AVERAGE(B1:B3)AVERAGEA関数
=AVERAGEA(数値)
数値:平均値を求める数値(複数指定可)
概要
AVERAGE関数と全く同じで平均値を返す関数。
AVERAGE関数とAVERAGEA関数の違いは、文字列を個数としてカウントするか否か。
AVERAGE関数は文字列が引数で与えられた場合、値0としてみなし、個数にも含めない。
AVERAGEA関数は文字列が引数で与えられた場合、値0としてみなし、個数に含める。
仮に引数が10,20,Aの場合
AVERAGE関数→ (10+20+0) / 2 = 15
AVERAGEA関数→ (10+20+0) / 3 = 10
となる
使用例

B4に設定されている式
=AVERAGEA(B1:B3)AVERAGEIF関数
=AVERAGEIF(数値,検索条件,[平均範囲])
数値:平均値を求める数値(範囲指定、複数可)
検索条件:対象となる条件
平均範囲:平均値を求める数値がある実際の範囲(範囲指定、複数可、省略可)
概要
平均値を求めるAVERAGE関数に条件をつけられるようになったもの。
例えば平均したいデータが表に有るが、その中から除外したいものがある場合は、このAVERAGEIF関数を使います。
第2引数の条件には、大なりや小なりを使用して条件をつけます。AND条件も可能。
第3引数は非常にわかりにくいのですが、これを指定すると指定した範囲が計算で使用されます。その場合第一引数の範囲は広さの定義に使われます。
例として、第一引数がA1:A3(3マス)、第3引数がC1:C5の場合にC1:C3が計算範囲になります。
つまり第一引数の形状が使われるということです。
使う場面としては動的に参照範囲を変えたい場合ですかね。
使用例

B4に設定されている式
=AVERAGEIF(B1:B3,">15")AVERAGEIFS関数
=AVERAGEIFS(平均範囲, 条件範囲 1, 条件 1, [条件範囲 2, 条件 2],)
平均範囲:平均値を求める数値のある範囲
条件範囲:条件の評価対象範囲範囲
条件:対象にする条件
概要
AVERAGEIF関数の条件を複数指定できるバージョンの関数。
引数は平均を求める範囲を指定した後は、条件範囲と条件をセットに設定していきます。
言うまでもなく平均値対象の抽出条件が2つ以上ある場合に使う形ですね。
ちなみに条件範囲と平均範囲は別の範囲を指定することが出来ます。

↑上記の場合ですと、C1:C4のうち3つ目のセルがfalseが返るので30は計算されません
使用例

B5に設定されている式
=AVERAGEIFS(B1:B4,B1:B4,">15",B1:B4,"<30")BAHTTEXT関数
=BAHTTEXT(数値)
数値:文字列に変換を行うタイ語の数値
概要
数値を入力すると、その数値をタイ語の文字列に変換してくれる関数。
タイ語を使うような仕事についていなければ絶対に使わないと思われる関数。おそらく自分が今後使うことは一切ないだろうw
ちなみに、数値から日本語に変換してくれる関数はないようです。日本語は漢字の扱いが結構面倒なのでタイ語よりこっちをやってくれよと思ってしまう。
例えば50000→五万とか結構需要はありそうな気がするのですが…。
使用例

B2に設定されている式
=BAHTTEXT(B1)BASE関数
=BASE(数値, 基数 ,[最大桁数])
数値:基数変換する数値
基数:変換する基数
最大桁数:返却する値の最大値(省略可)
概要
第一引数で指定した数値を、第二引数で指定した数値の基数に変換して返却をしてくれる関数。
第三引数は省略可能で、省略しなかった場合はこの値の桁数が返却値の最大桁数になります。
基数とは数値の数え方で2進数とか10進数とかです。
どの数値になったら桁が上がるかを表していて、例えば2進数だと2になったら桁が1つ上がるので、10進数の10を2進数に治すと
1010
になります。
使用例

B3に設定されている式
=BASE(B1,B2)BESSELI関数
=BESSELI(x,n)
x:数値
n:ベッセル関数における次数
概要
修正ベッセル関数の値を返却します。
まず修正ベッセル関数とか言うのが無学な自分は知りませんでした。
とりあえずwikiから抜粋してみる。
ベッセル関数(ベッセルかんすう、英: Bessel function)とは、最初にスイスの数学者ダニエル・ベルヌーイによって定義され、フリードリヒ・ヴィルヘルム・ベッセルにちなんで名づけられた関数。円筒関数と呼ばれることもある。以下に示す、ベッセルの微分方程式における特殊解の1つである。
https://ja.wikipedia.org/wiki/%E3%83%99%E3%83%83%E3%82%BB%E3%83%AB%E9%96%A2%E6%95%B0
なるほど、わからん。
微分方程式の解を求めるために使うということだろうか。
使用例

B3に設定されている式
=BESSELI(B1,B2)BESSELJ関数
=BESSELJ(x,n)
x:数値
n:ベッセル関数における次数
概要
こちらもベッセル関数に関わるものです。
(数学不得意すぎてギブアップ)
使用例

B3に設定されている式
=BESSELJ(B1,B2)BESSELK関数
=BESSELK(x,n)
x:数値
n:ベッセル関数における次数
概要
ベッセル関数に関する式が続いていて本当に泣きたいですw
(わからん)
これじゃ記事にしている意味がないですが…。
使用例

B3に設定されている式
=BESSELK(B1,B2)BESSELY関数
=BESSELY(x,n)
x:数値
n:ベッセル関数における次数
概要
ベッセル関数が続きます。
(やる気喪失)
使用例

B3に設定されている式
=BESSELK(B1,B2)











コメントを残す